Acitve learning 을 공부하면서, data 혹은 model 의 uncertainty 값을 잘 활용하면 모델 성능을 높일 수 있다는 것을 배웠다. data uncertainty 개념은 상대적으로 잘 이해됐는데, model uncertainty 에 대해서는 잘 이해되지 않아서 쓰는 글
Model uncertainty
우리가 학습시킨 인공지능이 내놓은 prediction 값이 얼마나 믿을만한 값인지 어떻게 알 수 있을까 ? 어떤 모델이 결정을 내릴 때 그 값이 얼마나 확실한지 ( certain ) 알아야 실생활에 사용될 어플리케이션 ( 예를 들면 자율 주행 ) 에 사용 가능할 것이다. 또 모델이 어떤 부분에서 certain 하고 어떤 부분에서는 uncertain 한지를 알고 있다면, 이 차이를 고려해서 실 app 에 사용시 최종 prediction 값을 활용할 수 있을 것이다.
Bayes’ Theorem
이런 uncertainty 를 정량화하는 방법 중 하나가 바로 베이지안의 정리이다.
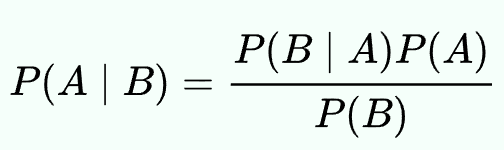
(1) Prior Probability
사전 확률은 관측 이후에 일어날 수 있는 다른 상황들을 고려하지 않은 채, 경험이나 직관에 의해 이미 알고 있는 것으로만 계산된 확률이다. 위 식에서는 원인 P(A) 에 해당한다.
(2) Posterior Probability
사후 확률은 P(A|B) 로, B 일 때 A 일 확률이 얼마나 되냐는 것 - 즉 결과 B 로부터 원인 A 가 무엇일지 역방향으로 생각하는 확률이다. 사후 확률은 새롭게 관찰된 근거들이 추가될때마다 확률분포가 계속해서 업데이트 된다.
(3) Bayes’ Theorem
Bayes의 정리는 사전 확률와 사후 확률 사이의 관계를 나타내는 정리를 말한다. 이 식을 활용해 사후 확률이 얼마인지 계산한다.
+ )
P(B|A) 는 A 일 때 B 일 확률 = likelihood probability
P(B) 는 B 일 확률 = Predictor prior probability
Bayesian neural network
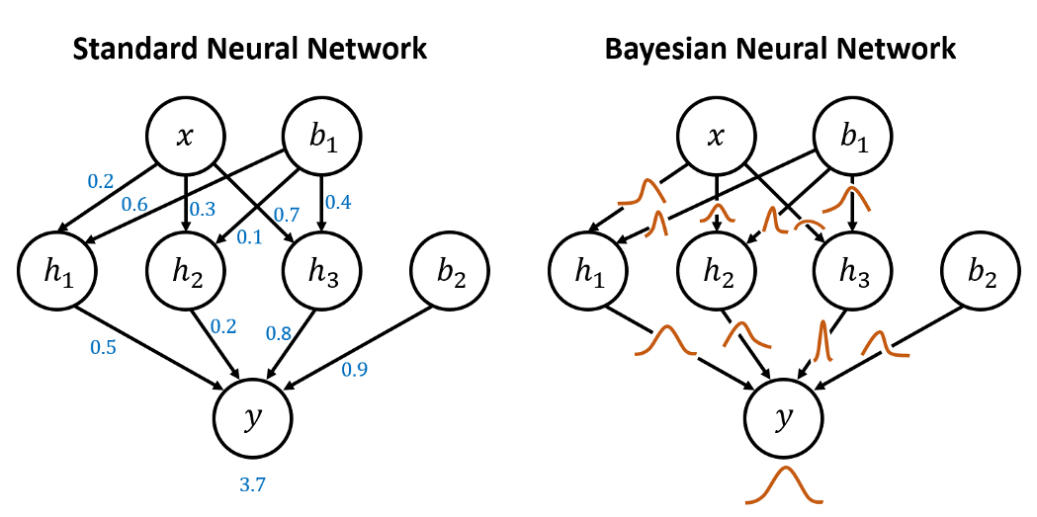
Bayesian neural network 는 베이즈 정리를 활용해서 학습하는 모델로, 모델 파라미터들의 분포를 학습한다. 훈련셋 X, Y 에 대해서 deterministic parameters 가 아닌, 모델 parameters 의 posterior distribution 를 학습하는 것이 Bayesian NN 의 목표이다. 즉, deterministic parameters = 우리가 일반적으로 모델을 학습한다고 하면 모델의 가중치 값이 변화하는 것을 생각한다. 그런데 Bayesian NN 는 모델의 가중치 값의 "분포"를 학습한다. 분포를 학습하기 때문에 비선형 함수를 학습하고, 불확실성도 표현할 수 있다.
Posterior probability 의 어려움
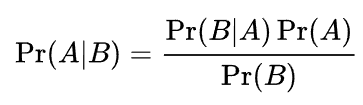
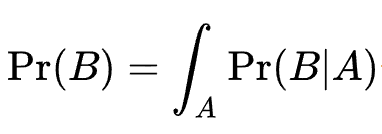
Posterior probability 는 실제로 측정하기 어려운 경우가 있다. Pr(B) 의 적분식을 계산해야하는데, 함수가 너무 고차원이 되거나 파라미터 수가 매우 많은 경우에는 이 식을 모두 계산하기 힘들기 때문이다. 이런 경우 이 값을 근사화해야 구할 수 있다.
Posterior distribution 근사화
마찬가지로, 베이지안 뉴럴넷에서도 posterior distribution 를 정확하게 계산하기 어렵다. 그래서 이 분포를 근사화해야한다. 근사화 방법은 크게 2가지로 나뉜다.
(1) 결정론적 방법 : Variational Inference
KL-divergence 및 ELBO 등
(2) 확률론적 방법 : MCMC ( Markov Chain Monte Carlo )
Monte Carlo Dropout 등
예측 결과
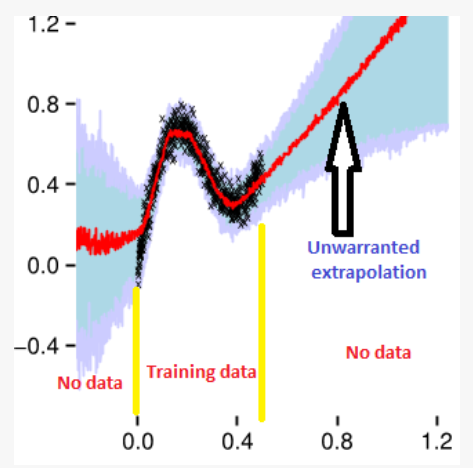
이렇게 학습한 베이지안 뉴럴넷으로 예측한 결과를 보면, 학습 데이터 이외에 다른 데이터로 predict 했을 때 불확실한 부분 ( 파란 부분 ) 이 늘어난 것을 확인할 수 있다.
다음 포스팅은 근사화 방법에 대해 더 자세히 다뤄보기로...
#참조
https://en.wikipedia.org/wiki/Bayes%27_theorem
http://www.ktword.co.kr/test/view/view.php?m_temp1=4215
https://bioinformaticsandme.tistory.com/47
https://ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%EC%A0%95%EB%A6%AC
https://gaussian37.github.io/dl-concept-bayesian_neural_network/
https://sanjaykthakur.com/2018/12/05/the-very-basics-of-bayesian-neural-networks/
https://simpling.tistory.com/25
https://stats.stackexchange.com/questions/271844/variational-inference-versus-mcmc-when-to-choose-one-over-the-other
'인공지능 > 이론 정리' 카테고리의 다른 글
| [Deep learning book] 5.1.2 The Performance Measure, P (0) | 2022.09.05 |
|---|---|
| [Deep learning book] 5.1.1 The Task, T (0) | 2022.09.04 |
| ActiveLearning (0) | 2022.07.09 |
| Convolution Layer 구현하기 (0) | 2022.03.06 |
| 오버피팅 방지와 하이퍼파라미터 최적화 (0) | 2022.02.16 |